擴展維納攻擊¶

• 擴展維納攻擊來自《Extending Wiener's Attack in the Presence of Many Decrypting Exponents》，相關題目在CTF中已經出現了，例如2020羊城杯的Simple，但都是一些模板題，這裏將詳細分析原論文中提出的方法以及分析方式，寫明擴展維納攻擊原理以及在文末給出了一些開放問題歡迎討論。

原理分析¶

維納（Wiener）的方法¶

• 維納Wiener提出了一種關於私鑰過小時對$N$進行分解的一種方式。並給出了證明當

  $$d < \frac{1}{3}N^{\frac{1}{4}}$$

  滿足時(還應滿足$q < p < 2q$，因這裏及後文主要是對私鑰進行探討，故忽略這類條件)一定能夠分解$N$。

• 以下爲原論文中對於Wiener's Approach的部分描述，部分內容有刪減，其實這裏也就是維納攻擊的證明，所以要想更詳細瞭解請再看維納攻擊的原理，這裏我們主要後面要用到這裏的式1。方法如下

  已知

  $$e*d -k*\lambda(N) = 1$$

  這裏$\lambda(N) = lcm(p-1, q-1) = \varphi(N) / g$，令$s = 1-p-q$則有

  $$edg - kN = g + ks\tag{1}$$

  將兩邊同時除以$dgN$則有

  $$\frac{e}{N} - \frac{k}{dg} = \frac{g+ks}{dgN} = (\frac{k}{dg})(\frac{s}{N}) + \frac{1}{dN}$$

  我們知道這裏有$e \approx N, s \approx N^{1/2}$，所以有$k/(dg)\approx 1$。則我們可以知道等式右邊約等於$N^{-1/2}$。我們都知道當

  $$|x - a/b| < 1/(2b^2)$$

  時則$a/b$是一個$x$連分數近似（連分數定理Continued Fractions）

  所以當

  $$d < \frac{\sqrt{2}}{2g}N^{\frac{1}{4}}$$

  時有$k/dg$是$e/N$的連分數近似，即能通過連分數展開覆蓋。

• 注意這裏前面所說的範圍和後面的範圍並不矛盾

  這裏對一些參數的值的近似並不嚴格，所以和維納攻擊的嚴格範圍有出入，具體細節可參考維納攻擊的證明。

郭（Guo）的方法¶

• 郭針對不止一個$e$的情況進行研究，但是郭只研究了兩個以及三個$e$的情況，上上節一樣，這裏我們還是使用原文內容翻譯+解釋的寫法。對於兩個$e$的情況，我們可以考慮

  $$e_1d_1g - k_1(p-1)(q-1) = g\\ e_2d_2g - k_2(p-1)(q-1) = g$$

  簡單化簡可以得到下式子

  $$k_2d_1e_1 - k_1d_2e_2 = k_2 - k_1\tag{2}$$

  兩邊同時除以$k_2d_1e_2$

  $$\frac{e_1}{e_2} - \frac{k_1d_2}{k_2d_1} = \frac{k_2 - k_1}{k_2d_1e_2}$$

  設$d_i < N^\alpha$，則等式右邊約等於$N^{-(1+\alpha)}$

  則當

  $$2(k_2d_1)^2 < N^{1+\alpha}$$

  時$k_1d_2/(k_2d_1)$是$e_1/e_2$的連分數近似。當$k_2$和$d_1$最多爲$N^\alpha$而且$g$很小時，得到

  $$\alpha < 1/3 - \epsilon\ \ \ (\epsilon > 0)$$

• 然而即使我們得到了$(k_1d_2)/(k_2d_1)$還是無法分解$N$，原文後面還討論了郭的提議，嘗試對$k_1d_2$進行分解，這裏不再講解。

擴展維納攻擊¶

• 上述部分內容截至目前（2021/10）網絡上已經有很多博文進行了講解了分析，但是對於具體擴展維納攻擊的原理以及格構造或者是更高維的推廣都沒有給出。這裏我將詳細的對原論文內容進行翻譯以及講解。

• 爲了將分析擴展到$n$個加密指數$e_i$（解密指數$d_i$很小），我們同時使用維納和郭的方法，我們將關係

  $$d_ige_i - k_iN = g + k_is$$

  記爲維納等式$W_i$，同樣我們可以得到關係

  $$k_id_je_j - k_jd_ie_i = k_i - k_j$$

  記爲郭等式$G_{i,j}$。

  我們假設$d_i$和$k_i$都小於$N^{\alpha_n}$，且$g$很小，$s \approx N^{1/2}$。可以注意到$W_i$和$G_i$的右側非常小，實際上分別最多爲$N^{1/2 + \alpha}$和$N^\alpha$。

  最後，我們考慮複合關係式比如$W_uG_{v,w}$，顯然大小爲$N^{1/2 + 2\alpha}$。

• 原文中這裏是定義了兩個關係式以及指出了他們的大小範圍，這個範圍很重要也容容易分析處理，之後我們所做的其實就是使用這兩個式子的不同複合關係去構造一個格，然後通過求其基向量得到$d_1g/k_1$，從而可以算得$\varphi(N)$並可以進一步的對$N$進行分解。

• 其實到這裏原理分析已經結束，關於格的構造其實也並不複雜，但是核心是這裏的複合關係的選取，以及對於最後$\alpha$大小的分析。

兩個小解密指數的情況¶

• 我們選取關係$W_1, G_{1,2},W_1W_2$,這樣便有

  $$\begin{aligned} d_1ge_1 - k_1N &= g+k_1s\\ k_1d_2e_2 - k_2d_1e_1 &= k_1-k_2\\ d_1d_2g^2e_1e_2 - d_1gk_2e_1N - d_2gk_1e_2N + k_1k_2N^2 &= (g+k_1s)(g+k_2s) \end{aligned}$$

  我們對第一個關係式乘上$k_2$，這樣左邊便全是由$d_1d_2g^2, d_1gk_2, d_2gk_1$和$k_1k_2$構成，這樣我們便可以用已知內容構造格將上述式子轉化爲矩陣運算

  $$\begin{pmatrix} k_1k_2&d_1gk_2&d_2gk_1&d_1d_2g^2 \end{pmatrix} \begin{pmatrix} 1&-N&0&N^2\\ &e_1&-e_1&-e_1N\\ &&e_2&-e_2N\\ &&&e_1e_2 \end{pmatrix} = \begin{pmatrix} k_1k_2&k_2(g+k_1s)&g(k_1 - k_2)&(g+k_1s)(g+k_2s) \end{pmatrix}$$

  等式右邊向量的大小爲$N^{2\alpha_2}, N^{1/2+2\alpha_2}, N^{\alpha_2}, N^{1+2\alpha_2}$,爲了讓大小相等，我們可以考慮構造一個D矩陣。

  $$D = \begin{pmatrix} N&&&\\ &N^{1/2}&&\\ &&N^{1+\alpha_2}&\\ &&&1 \end{pmatrix}$$

  最終我們構造的矩陣爲

  $$L_2 = \begin{pmatrix} 1&-N&0&N^2\\ &e_1&-e_1&-e_1N\\ &&e_2&-e_2N\\ &&&e_1e_2 \end{pmatrix} * D$$

  這樣向量$b = \begin{pmatrix} k_1k_2&d_1gk_2&d_2gk_1&d_1d_2g^2 \end{pmatrix}$便有

  $$\Vert bL_2 \Vert < 2N^{1+2\alpha_2}$$

  這也就是爲什麼前面需要構造$D$矩陣的原因，給定$D$矩陣後，我們可以得到一個上界，這樣問題可以轉化爲類SVP問題。

  那麼這裏的b向量其實我們使用格基規約算法例如LLL便可以得到基向量$b$，然後我們求解$b_2/b_1$即得到$d_1g/k_1$

  之後我們就可以得到

  $$\varphi(N) = \frac{edg}{k} - \frac{g}{k} = \lfloor edg/k\rceil$$

  我們假設這些格中最短向量長度爲$\Delta^{1/4-\epsilon}$，其中$\Delta = det(L_2) = N^{13/2 + \alpha_2}$。如果這些格是隨機的，我們甚至幾乎可以肯定沒有格點比閔可夫斯基界（Minkowski's bound）$2\Delta^{1/4}$，所以$bL_2$是最短向量當

  $$N^{1+2\alpha_2} < (1/c_2)\left(N^{13/2+\alpha_2}\right)^{1/4}$$

  對於一些小的$c_2$，如果有

  $$\alpha_2 < 5/14 - \epsilon^{'}$$

  則我們可以通過格基規約找到向量$b$。

• 上述內容是原文中給出的當兩個小解密指數是進行的攻擊細節，並且分析了$\alpha$的大小關係。

三個小解密指數的情況¶

• 對於三個指數的情況我們額外選取$G_{1, 3}, W_1G_{2, 3}, W_2G_{1,3}$

  這樣我們的向量b爲

  $$B = \begin{pmatrix} k_1k_2k_3&d_1gk_2k_3&k_1d_2gk_3&d_1d_2g^2k_3&k_1k_2d_3g&k_1d_3g&k_2d_3g&d_1d_2d_3g^3 \end{pmatrix}$$

  然後我們便可以構造格

  $$L_3 = \left(\begin{array}{rrrrrrrr} 1 & -N & 0 & N^{2} & 0 & 0 & 0 & -N^{3} \\ 0 & e_{1} & -e_{1} & -N e_{1} & -e_{1} & 0 & N e_{1} & N^{2} e_{1} \\ 0 & 0 & e_{2} & -N e_{2} & 0 & N e_{2} & 0 & N^{2} e_{2} \\ 0 & 0 & 0 & e_{1} e_{2} & 0 & -e_{1} e_{2} & -e_{1} e_{2} & -N e_{1} e_{2} \\ 0 & 0 & 0 & 0 & e_{3} & -N e_{3} & -N e_{3} & N^{2} e_{3} \\ 0 & 0 & 0 & 0 & 0 & e_{1} e_{3} & 0 & -N e_{1} e_{3} \\ 0 & 0 & 0 & 0 & 0 & 0 & e_{2} e_{3} & -N e_{2} e_{3} \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & e_{1} e_{2} e_{3} \end{array}\right)$$

  其中

  $$D = diag(\begin{array}{r} N^{\frac{3}{2}}&N&N^{a + \frac{3}{2}}&\sqrt{N}&N^{a + \frac{3}{2}}&N^{a + 1}&N^{a + 1}&1\end{array})$$

  同樣我們可以得到

  $$\Vert bL_2 \Vert < \sqrt{8}N^{3/2+2\alpha_3}$$

  則當

  $$\alpha_3 < 2/5 - \epsilon^{'}$$

  時可以通過格基規約求出向量$b$。

四個小解密指數的情況¶

• 額外選取$G_{1, 4}, W_1G_{2, 4}, G_{1, 2}G_{3,4}, G_{1, 3}G_{2, 4}, W_1W_2G_{3, 4}, W_1W_3G_{2, 4}, W_2W_3G_{1, 4}, W_1W_2W_3W_4$進行構造。不再翻譯。

分析¶

• 擴展維納攻擊結合上述三個例子已經詳細的闡明瞭方法細節，但是其中沒有講解如何選取複合關係。其實在原文的附錄中給出了複合關係的選取，以及給出了$\alpha_n$的表達式。

• 在原文附錄部分，考慮$n$個指數$e_i$，這樣則有$2^n$個不同的量$h_j$（一個表達式$e_i$的個數），這樣我們的$L_n$在乘上$D$之前，矩陣$L_n$的行列式爲$N^{n2^{n-1}}$

  這樣最後一個關係$W_1W_2\dots W_n$最大爲$N^{n/2 + n\alpha_n}$，這樣我們便知道了任意情況的最大界值，我們只需要讓其他值增加到這麼多即可（即構造$D$矩陣）

  引入了新的關係式

  $$R_{u,v} = W_{i_1}\dots W_{i_u}G_{j_1, l_1}\dots G_{j_v, l_v}$$

  其中$i_1,\dots,i_u,j_1,\dots,j_u,l_1,\dots,l_v$都不同，那麼這裏最多會有$u + 2v$個指數$e_i$，則我們的關係$R_{u,v}$最多爲$N^{u/2 + (u+v)\alpha_n}$，同時注意我要需要所有係數的大小大致相同，所以我們在某些等式乘上$k_i$，使得關係$R_{u, v} = N^{u/2 + (n-v)\alpha_n}$。

  最後我們再計算所有的大小與最大大小$N^{n/2 + n\alpha_n}$的差值，構造矩陣$D$。

  這樣我們便完成了矩陣$D$的構造，同時設矩陣$D$裏面指數的乘積爲$\beta_n = x+y\alpha_n$，這樣有

  $$det(L_n) \approx N^{n2^{n-1} + x + y\alpha_n}$$

  則有

  $$N^{n/2 + n\alpha_n} < (1/c_n)\left(N^{n2^{n-1} + x + y\alpha_n}\right)^{1/2^n}$$

  對於小$c_n$，有

  $$\alpha_n < \frac{x}{n2^n - y} - \epsilon^{'}$$

  所以我們要想讓$\alpha_n$更大就需要讓$x$和$y$更大，這意味着我們要選取更多的$v$和更小的$u$。比如在$n=2$的情況我們選取$W_1, G_{1, 2}, W_1W_2$而不是$W_1, W_2, W_1W_2$因爲前者$\beta_2 = 5/2 + \alpha$而後者$\beta_2 = 2$。

• 到這裏，其實已經講清楚了擴展維納攻擊的整個流程，如何選擇複合關係，如何構造格，如何構造矩陣$D$以及如何求解。在原文的文末也給出了$n\le 5$時候的選擇關係表。

  

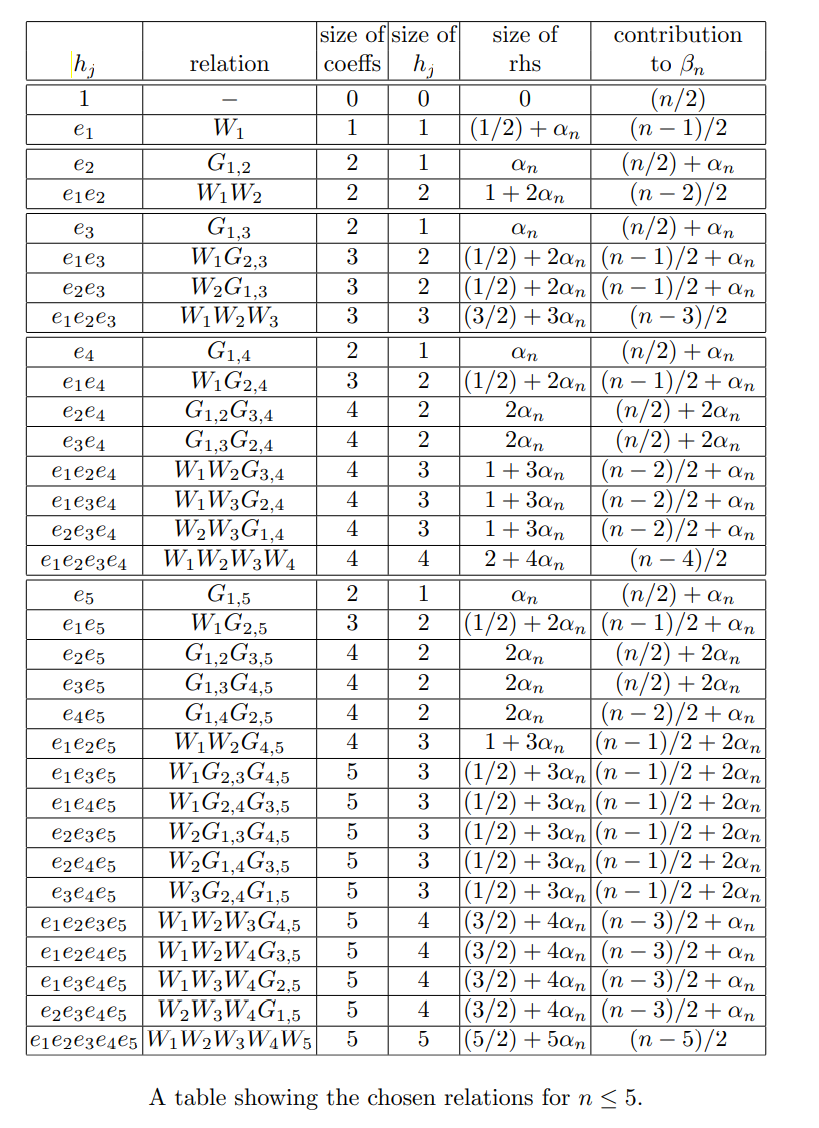
  這裏我也給出$n\le8$的選擇關係以及$n=6$時候構造的矩陣以供驗證自己是否能夠編寫出選擇關係式的邏輯代碼。

  -
  W(1)
  G(1, 2)
  W(1)W(2)
  G(1, 3)
  W(1)G(2, 3)
  W(2)G(1, 3)
  W(1)W(2)W(3)
  G(1, 4)
  W(1)G(2, 4)
  G(1, 2)G(3, 4)
  G(1, 3)G(2, 4)
  W(1)W(2)G(3, 4)
  W(1)W(3)G(2, 4)
  W(2)W(3)G(1, 4)
  W(1)W(2)W(3)W(4)
  G(1, 5)
  W(1)G(2, 5)
  G(1, 2)G(3, 5)
  G(1, 3)G(2, 5)
  G(1, 4)G(2, 5)
  W(1)W(2)G(3, 5)
  W(1)G(2, 3)G(4, 5)
  W(1)G(2, 4)G(3, 5)
  W(2)G(1, 3)G(4, 5)
  W(2)G(1, 4)G(3, 5)
  W(3)G(1, 4)G(2, 5)
  W(1)W(2)W(3)G(4, 5)
  W(1)W(2)W(4)G(3, 5)
  W(1)W(3)W(4)G(2, 5)
  W(2)W(3)W(4)G(1, 5)
  W(1)W(2)W(3)W(4)W(5)
  G(1, 6)
  W(1)G(2, 6)
  G(1, 2)G(3, 6)
  G(1, 3)G(2, 6)
  G(1, 4)G(2, 6)
  G(1, 5)G(2, 6)
  W(1)W(2)G(3, 6)
  W(1)G(2, 3)G(4, 6)
  W(1)G(2, 4)G(3, 6)
  W(1)G(2, 5)G(3, 6)
  G(1, 2)W(3)G(4, 6)
  G(1, 2)G(3, 4)G(5, 6)
  G(1, 2)G(3, 5)G(4, 6)
  G(1, 3)G(2, 4)G(5, 6)
  G(1, 3)G(2, 5)G(4, 6)
  G(1, 4)G(2, 5)G(3, 6)
  W(1)W(2)W(3)G(4, 6)
  W(1)W(2)G(3, 4)G(5, 6)
  W(1)W(2)G(3, 5)G(4, 6)
  W(1)W(3)G(2, 4)G(5, 6)
  W(1)W(3)G(2, 5)G(4, 6)
  W(1)W(4)G(2, 5)G(3, 6)
  W(2)W(3)G(1, 4)G(5, 6)
  W(2)W(3)G(1, 5)G(4, 6)
  W(2)W(4)G(1, 5)G(3, 6)
  W(3)W(4)G(1, 5)G(2, 6)
  W(1)W(2)W(3)W(4)G(5, 6)
  W(1)W(2)W(3)W(5)G(4, 6)
  W(1)W(2)W(4)W(5)G(3, 6)
  W(1)W(3)W(4)W(5)G(2, 6)
  W(2)W(3)W(4)W(5)G(1, 6)
  W(1)W(2)W(3)W(4)W(5)W(6)
  G(1, 7)
  W(1)G(2, 7)
  G(1, 2)G(3, 7)
  G(1, 3)G(2, 7)
  G(1, 4)G(2, 7)
  G(1, 5)G(2, 7)
  G(1, 6)G(2, 7)
  W(1)W(2)G(3, 7)
  W(1)G(2, 3)G(4, 7)
  W(1)G(2, 4)G(3, 7)
  W(1)G(2, 5)G(3, 7)
  W(1)G(2, 6)G(3, 7)
  G(1, 2)W(3)G(4, 7)
  G(1, 2)G(3, 4)G(5, 7)
  G(1, 2)G(3, 5)G(4, 7)
  G(1, 2)G(3, 6)G(4, 7)
  G(1, 3)G(2, 4)G(5, 7)
  G(1, 3)G(2, 5)G(4, 7)
  G(1, 3)G(2, 6)G(4, 7)
  G(1, 4)G(2, 5)G(3, 7)
  G(1, 4)G(2, 6)G(3, 7)
  G(1, 5)G(2, 6)G(3, 7)
  W(1)W(2)W(3)G(4, 7)
  W(1)W(2)G(3, 4)G(5, 7)
  W(1)W(2)G(3, 5)G(4, 7)
  W(1)W(2)G(3, 6)G(4, 7)
  W(1)G(2, 3)W(4)G(5, 7)
  W(1)G(2, 3)G(4, 5)G(6, 7)
  W(1)G(2, 3)G(4, 6)G(5, 7)
  W(1)G(2, 4)G(3, 5)G(6, 7)
  W(1)G(2, 4)G(3, 6)G(5, 7)
  W(1)G(2, 5)G(3, 6)G(4, 7)
  W(2)G(1, 3)W(4)G(5, 7)
  W(2)G(1, 3)G(4, 5)G(6, 7)
  W(2)G(1, 3)G(4, 6)G(5, 7)
  W(2)G(1, 4)G(3, 5)G(6, 7)
  W(2)G(1, 4)G(3, 6)G(5, 7)
  W(2)G(1, 5)G(3, 6)G(4, 7)
  W(3)G(1, 4)G(2, 5)G(6, 7)
  W(3)G(1, 4)G(2, 6)G(5, 7)
  W(3)G(1, 5)G(2, 6)G(4, 7)
  W(4)G(1, 5)G(2, 6)G(3, 7)
  W(1)W(2)W(3)W(4)G(5, 7)
  W(1)W(2)W(3)G(4, 5)G(6, 7)
  W(1)W(2)W(3)G(4, 6)G(5, 7)
  W(1)W(2)W(4)G(3, 5)G(6, 7)
  W(1)W(2)W(4)G(3, 6)G(5, 7)
  W(1)W(2)W(5)G(3, 6)G(4, 7)
  W(1)W(3)W(4)G(2, 5)G(6, 7)
  W(1)W(3)W(4)G(2, 6)G(5, 7)
  W(1)W(3)W(5)G(2, 6)G(4, 7)
  W(1)W(4)W(5)G(2, 6)G(3, 7)
  W(2)W(3)W(4)G(1, 5)G(6, 7)
  W(2)W(3)W(4)G(1, 6)G(5, 7)
  W(2)W(3)W(5)G(1, 6)G(4, 7)
  W(2)W(4)W(5)G(1, 6)G(3, 7)
  W(3)W(4)W(5)G(1, 6)G(2, 7)
  W(1)W(2)W(3)W(4)W(5)G(6, 7)
  W(1)W(2)W(3)W(4)W(6)G(5, 7)
  W(1)W(2)W(3)W(5)W(6)G(4, 7)
  W(1)W(2)W(4)W(5)W(6)G(3, 7)
  W(1)W(3)W(4)W(5)W(6)G(2, 7)
  W(2)W(3)W(4)W(5)W(6)G(1, 7)
  W(1)W(2)W(3)W(4)W(5)W(6)W(7)
  G(1, 8)
  W(1)G(2, 8)
  G(1, 2)G(3, 8)
  G(1, 3)G(2, 8)
  G(1, 4)G(2, 8)
  G(1, 5)G(2, 8)
  G(1, 6)G(2, 8)
  G(1, 7)G(2, 8)
  W(1)W(2)G(3, 8)
  W(1)G(2, 3)G(4, 8)
  W(1)G(2, 4)G(3, 8)
  W(1)G(2, 5)G(3, 8)
  W(1)G(2, 6)G(3, 8)
  W(1)G(2, 7)G(3, 8)
  G(1, 2)W(3)G(4, 8)
  G(1, 2)G(3, 4)G(5, 8)
  G(1, 2)G(3, 5)G(4, 8)
  G(1, 2)G(3, 6)G(4, 8)
  G(1, 2)G(3, 7)G(4, 8)
  G(1, 3)G(2, 4)G(5, 8)
  G(1, 3)G(2, 5)G(4, 8)
  G(1, 3)G(2, 6)G(4, 8)
  G(1, 3)G(2, 7)G(4, 8)
  G(1, 4)G(2, 5)G(3, 8)
  G(1, 4)G(2, 6)G(3, 8)
  G(1, 4)G(2, 7)G(3, 8)
  G(1, 5)G(2, 6)G(3, 8)
  G(1, 5)G(2, 7)G(3, 8)
  G(1, 6)G(2, 7)G(3, 8)
  W(1)W(2)W(3)G(4, 8)
  W(1)W(2)G(3, 4)G(5, 8)
  W(1)W(2)G(3, 5)G(4, 8)
  W(1)W(2)G(3, 6)G(4, 8)
  W(1)W(2)G(3, 7)G(4, 8)
  W(1)G(2, 3)W(4)G(5, 8)
  W(1)G(2, 3)G(4, 5)G(6, 8)
  W(1)G(2, 3)G(4, 6)G(5, 8)
  W(1)G(2, 3)G(4, 7)G(5, 8)
  W(1)G(2, 4)G(3, 5)G(6, 8)
  W(1)G(2, 4)G(3, 6)G(5, 8)
  W(1)G(2, 4)G(3, 7)G(5, 8)
  W(1)G(2, 5)G(3, 6)G(4, 8)
  W(1)G(2, 5)G(3, 7)G(4, 8)
  W(1)G(2, 6)G(3, 7)G(4, 8)
  G(1, 2)W(3)W(4)G(5, 8)
  G(1, 2)W(3)G(4, 5)G(6, 8)
  G(1, 2)W(3)G(4, 6)G(5, 8)
  G(1, 2)W(3)G(4, 7)G(5, 8)
  G(1, 2)G(3, 4)W(5)G(6, 8)
  G(1, 2)G(3, 4)G(5, 6)G(7, 8)
  G(1, 2)G(3, 4)G(5, 7)G(6, 8)
  G(1, 2)G(3, 5)G(4, 6)G(7, 8)
  G(1, 2)G(3, 5)G(4, 7)G(6, 8)
  G(1, 2)G(3, 6)G(4, 7)G(5, 8)
  G(1, 3)G(2, 4)W(5)G(6, 8)
  G(1, 3)G(2, 4)G(5, 6)G(7, 8)
  G(1, 3)G(2, 4)G(5, 7)G(6, 8)
  G(1, 3)G(2, 5)G(4, 6)G(7, 8)
  G(1, 3)G(2, 5)G(4, 7)G(6, 8)
  G(1, 3)G(2, 6)G(4, 7)G(5, 8)
  G(1, 4)G(2, 5)G(3, 6)G(7, 8)
  G(1, 4)G(2, 5)G(3, 7)G(6, 8)
  G(1, 4)G(2, 6)G(3, 7)G(5, 8)
  G(1, 5)G(2, 6)G(3, 7)G(4, 8)
  W(1)W(2)W(3)W(4)G(5, 8)
  W(1)W(2)W(3)G(4, 5)G(6, 8)
  W(1)W(2)W(3)G(4, 6)G(5, 8)
  W(1)W(2)W(3)G(4, 7)G(5, 8)
  W(1)W(2)G(3, 4)W(5)G(6, 8)
  W(1)W(2)G(3, 4)G(5, 6)G(7, 8)
  W(1)W(2)G(3, 4)G(5, 7)G(6, 8)
  W(1)W(2)G(3, 5)G(4, 6)G(7, 8)
  W(1)W(2)G(3, 5)G(4, 7)G(6, 8)
  W(1)W(2)G(3, 6)G(4, 7)G(5, 8)
  W(1)W(3)G(2, 4)W(5)G(6, 8)
  W(1)W(3)G(2, 4)G(5, 6)G(7, 8)
  W(1)W(3)G(2, 4)G(5, 7)G(6, 8)
  W(1)W(3)G(2, 5)G(4, 6)G(7, 8)
  W(1)W(3)G(2, 5)G(4, 7)G(6, 8)
  W(1)W(3)G(2, 6)G(4, 7)G(5, 8)
  W(1)W(4)G(2, 5)G(3, 6)G(7, 8)
  W(1)W(4)G(2, 5)G(3, 7)G(6, 8)
  W(1)W(4)G(2, 6)G(3, 7)G(5, 8)
  W(1)W(5)G(2, 6)G(3, 7)G(4, 8)
  W(2)W(3)G(1, 4)W(5)G(6, 8)
  W(2)W(3)G(1, 4)G(5, 6)G(7, 8)
  W(2)W(3)G(1, 4)G(5, 7)G(6, 8)
  W(2)W(3)G(1, 5)G(4, 6)G(7, 8)
  W(2)W(3)G(1, 5)G(4, 7)G(6, 8)
  W(2)W(3)G(1, 6)G(4, 7)G(5, 8)
  W(2)W(4)G(1, 5)G(3, 6)G(7, 8)
  W(2)W(4)G(1, 5)G(3, 7)G(6, 8)
  W(2)W(4)G(1, 6)G(3, 7)G(5, 8)
  W(2)W(5)G(1, 6)G(3, 7)G(4, 8)
  W(3)W(4)G(1, 5)G(2, 6)G(7, 8)
  W(3)W(4)G(1, 5)G(2, 7)G(6, 8)
  W(3)W(4)G(1, 6)G(2, 7)G(5, 8)
  W(3)W(5)G(1, 6)G(2, 7)G(4, 8)
  W(4)W(5)G(1, 6)G(2, 7)G(3, 8)
  W(1)W(2)W(3)W(4)W(5)G(6, 8)
  W(1)W(2)W(3)W(4)G(5, 6)G(7, 8)
  W(1)W(2)W(3)W(4)G(5, 7)G(6, 8)
  W(1)W(2)W(3)W(5)G(4, 6)G(7, 8)
  W(1)W(2)W(3)W(5)G(4, 7)G(6, 8)
  W(1)W(2)W(3)W(6)G(4, 7)G(5, 8)
  W(1)W(2)W(4)W(5)G(3, 6)G(7, 8)
  W(1)W(2)W(4)W(5)G(3, 7)G(6, 8)
  W(1)W(2)W(4)W(6)G(3, 7)G(5, 8)
  W(1)W(2)W(5)W(6)G(3, 7)G(4, 8)
  W(1)W(3)W(4)W(5)G(2, 6)G(7, 8)
  W(1)W(3)W(4)W(5)G(2, 7)G(6, 8)
  W(1)W(3)W(4)W(6)G(2, 7)G(5, 8)
  W(1)W(3)W(5)W(6)G(2, 7)G(4, 8)
  W(1)W(4)W(5)W(6)G(2, 7)G(3, 8)
  W(2)W(3)W(4)W(5)G(1, 6)G(7, 8)
  W(2)W(3)W(4)W(5)G(1, 7)G(6, 8)
  W(2)W(3)W(4)W(6)G(1, 7)G(5, 8)
  W(2)W(3)W(5)W(6)G(1, 7)G(4, 8)
  W(2)W(4)W(5)W(6)G(1, 7)G(3, 8)
  W(3)W(4)W(5)W(6)G(1, 7)G(2, 8)
  W(1)W(2)W(3)W(4)W(5)W(6)G(7, 8)
  W(1)W(2)W(3)W(4)W(5)W(7)G(6, 8)
  W(1)W(2)W(3)W(4)W(6)W(7)G(5, 8)
  W(1)W(2)W(3)W(5)W(6)W(7)G(4, 8)
  W(1)W(2)W(4)W(5)W(6)W(7)G(3, 8)
  W(1)W(3)W(4)W(5)W(6)W(7)G(2, 8)
  W(2)W(3)W(4)W(5)W(6)W(7)G(1, 8)
  W(1)W(2)W(3)W(4)W(5)W(6)W(7)W(8)
  

  $$\left(\begin{array}{rrrrrrrrrrrrrrrrrrrrrrrrrrrrrrrrrrrrrrrrrrrrrrrrrrrrrrrrrrrrrrrr} 1 & -N & 0 & N^{2} & 0 & 0 & 0 & -N^{3} & 0 & 0 & 0 & 0 & 0 & 0 & 0 & N^{4} & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & -N^{5} & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & N^{6} \\ 0 & e_{1} & -e_{1} & -N e_{1} & -e_{1} & 0 & N e_{1} & N^{2} e_{1} & -e_{1} & 0 & 0 & 0 & 0 & 0 & -N^{2} e_{1} & -N^{3} e_{1} & -e_{1} & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & N^{3} e_{1} & N^{4} e_{1} & -e_{1} & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & -N^{4} e_{1} & -N^{5} e_{1} \\ 0 & 0 & e_{2} & -N e_{2} & 0 & N e_{2} & 0 & N^{2} e_{2} & 0 & N e_{2} & 0 & 0 & 0 & -N^{2} e_{2} & 0 & -N^{3} e_{2} & 0 & N e_{2} & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & N^{3} e_{2} & 0 & N^{4} e_{2} & 0 & N e_{2} & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & -N^{4} e_{2} & 0 & -N^{5} e_{2} \\ 0 & 0 & 0 & e_{1} e_{2} & 0 & -e_{1} e_{2} & -e_{1} e_{2} & -N e_{1} e_{2} & 0 & -e_{1} e_{2} & 0 & e_{1} e_{2} & 0 & N e_{1} e_{2} & N e_{1} e_{2} & N^{2} e_{1} e_{2} & 0 & -e_{1} e_{2} & 0 & e_{1} e_{2} & e_{1} e_{2} & 0 & 0 & 0 & 0 & 0 & -N e_{1} e_{2} & 0 & 0 & -N^{2} e_{1} e_{2} & -N^{2} e_{1} e_{2} & -N^{3} e_{1} e_{2} & 0 & -e_{1} e_{2} & 0 & e_{1} e_{2} & e_{1} e_{2} & e_{1} e_{2} & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & N^{2} e_{1} e_{2} & 0 & 0 & 0 & N^{3} e_{1} e_{2} & N^{3} e_{1} e_{2} & N^{4} e_{1} e_{2} \\ 0 & 0 & 0 & 0 & e_{3} & -N e_{3} & -N e_{3} & N^{2} e_{3} & 0 & 0 & 0 & 0 & -N^{2} e_{3} & 0 & 0 & -N^{3} e_{3} & 0 & 0 & 0 & 0 & 0 & -N^{2} e_{3} & 0 & 0 & 0 & 0 & 0 & 0 & N^{3} e_{3} & 0 & 0 & N^{4} e_{3} & 0 & 0 & 0 & 0 & 0 & 0 & -N^{2} e_{3} & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & -N^{4} e_{3} & 0 & 0 & -N^{5} e_{3} \\ 0 & 0 & 0 & 0 & 0 & e_{1} e_{3} & 0 & -N e_{1} e_{3} & 0 & 0 & e_{1} e_{3} & 0 & N e_{1} e_{3} & 0 & N e_{1} e_{3} & N^{2} e_{1} e_{3} & 0 & 0 & e_{1} e_{3} & 0 & 0 & N e_{1} e_{3} & 0 & 0 & 0 & -N e_{1} e_{3} & 0 & 0 & -N^{2} e_{1} e_{3} & 0 & -N^{2} e_{1} e_{3} & -N^{3} e_{1} e_{3} & 0 & 0 & e_{1} e_{3} & 0 & 0 & 0 & N e_{1} e_{3} & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & N^{2} e_{1} e_{3} & 0 & 0 & 0 & N^{3} e_{1} e_{3} & 0 & N^{3} e_{1} e_{3} & N^{4} e_{1} e_{3} \\ 0 & 0 & 0 & 0 & 0 & 0 & e_{2} e_{3} & -N e_{2} e_{3} & 0 & 0 & -e_{2} e_{3} & -e_{2} e_{3} & N e_{2} e_{3} & N e_{2} e_{3} & 0 & N^{2} e_{2} e_{3} & 0 & 0 & -e_{2} e_{3} & -e_{2} e_{3} & 0 & N e_{2} e_{3} & 0 & -N e_{2} e_{3} & 0 & 0 & 0 & 0 & -N^{2} e_{2} e_{3} & -N^{2} e_{2} e_{3} & 0 & -N^{3} e_{2} e_{3} & 0 & 0 & -e_{2} e_{3} & -e_{2} e_{3} & 0 & 0 & N e_{2} e_{3} & 0 & -N e_{2} e_{3} & -N e_{2} e_{3} & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & N^{2} e_{2} e_{3} & 0 & 0 & 0 & 0 & 0 & 0 & N^{3} e_{2} e_{3} & N^{3} e_{2} e_{3} & 0 & N^{4} e_{2} e_{3} \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & e_{1} e_{2} e_{3} & 0 & 0 & 0 & 0 & -e_{1} e_{2} e_{3} & -e_{1} e_{2} e_{3} & -e_{1} e_{2} e_{3} & -N e_{1} e_{2} e_{3} & 0 & 0 & 0 & 0 & 0 & -e_{1} e_{2} e_{3} & 0 & e_{1} e_{2} e_{3} & 0 & e_{1} e_{2} e_{3} & e_{1} e_{2} e_{3} & 0 & N e_{1} e_{2} e_{3} & N e_{1} e_{2} e_{3} & N e_{1} e_{2} e_{3} & N^{2} e_{1} e_{2} e_{3} & 0 & 0 & 0 & 0 & 0 & 0 & -e_{1} e_{2} e_{3} & 0 & e_{1} e_{2} e_{3} & e_{1} e_{2} e_{3} & 0 & 0 & 0 & 0 & 0 & -e_{1} e_{2} e_{3} & 0 & 0 & 0 & 0 & 0 & -N e_{1} e_{2} e_{3} & 0 & 0 & -N e_{1} e_{2} e_{3} & -N e_{1} e_{2} e_{3} & 0 & 0 & -N^{2} e_{1} e_{2} e_{3} & -N^{2} e_{1} e_{2} e_{3} & -N^{2} e_{1} e_{2} e_{3} & -N^{3} e_{1} e_{2} e_{3} \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & e_{4} & -N e_{4} & 0 & 0 & N^{2} e_{4} & N^{2} e_{4} & N^{2} e_{4} & -N^{3} e_{4} & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & N^{3} e_{4} & 0 & 0 & 0 & N^{4} e_{4} & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & N^{3} e_{4} & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & -N^{4} e_{4} & 0 & 0 & 0 & -N^{5} e_{4} \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & e_{1} e_{4} & -e_{1} e_{4} & -e_{1} e_{4} & -N e_{1} e_{4} & -N e_{1} e_{4} & 0 & N^{2} e_{1} e_{4} & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & -N e_{1} e_{4} & 0 & 0 & -N^{2} e_{1} e_{4} & 0 & 0 & -N^{2} e_{1} e_{4} & -N^{3} e_{1} e_{4} & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & -N e_{1} e_{4} & 0 & 0 & 0 & 0 & 0 & -N^{2} e_{1} e_{4} & 0 & 0 & 0 & 0 & 0 & 0 & N^{2} e_{1} e_{4} & 0 & 0 & 0 & N^{3} e_{1} e_{4} & 0 & 0 & N^{3} e_{1} e_{4} & N^{4} e_{1} e_{4} \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & e_{2} e_{4} & 0 & -N e_{2} e_{4} & 0 & -N e_{2} e_{4} & N^{2} e_{2} e_{4} & 0 & 0 & 0 & 0 & -e_{2} e_{4} & 0 & -N e_{2} e_{4} & 0 & 0 & 0 & N e_{2} e_{4} & -N^{2} e_{2} e_{4} & 0 & -N^{2} e_{2} e_{4} & 0 & -N^{3} e_{2} e_{4} & 0 & 0 & 0 & 0 & -e_{2} e_{4} & 0 & 0 & -N e_{2} e_{4} & 0 & 0 & N e_{2} e_{4} & 0 & 0 & 0 & 0 & 0 & -N^{2} e_{2} e_{4} & 0 & 0 & 0 & N^{2} e_{2} e_{4} & 0 & 0 & 0 & 0 & 0 & 0 & N^{3} e_{2} e_{4} & 0 & N^{3} e_{2} e_{4} & 0 & N^{4} e_{2} e_{4} \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & e_{3} e_{4} & 0 & -N e_{3} e_{4} & -N e_{3} e_{4} & N^{2} e_{3} e_{4} & 0 & 0 & 0 & 0 & 0 & 0 & N e_{3} e_{4} & N e_{3} e_{4} & N e_{3} e_{4} & N e_{3} e_{4} & 0 & -N^{2} e_{3} e_{4} & -N^{2} e_{3} e_{4} & 0 & 0 & -N^{3} e_{3} e_{4} & 0 & 0 & 0 & 0 & 0 & 0 & 0 & N e_{3} e_{4} & N e_{3} e_{4} & 0 & 0 & 0 & 0 & 0 & 0 & 0 & -N^{2} e_{3} e_{4} & 0 & N^{2} e_{3} e_{4} & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & N^{3} e_{3} e_{4} & N^{3} e_{3} e_{4} & 0 & 0 & N^{4} e_{3} e_{4} \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & e_{1} e_{2} e_{4} & 0 & 0 & -N e_{1} e_{2} e_{4} & 0 & 0 & 0 & 0 & 0 & 0 & e_{1} e_{2} e_{4} & 0 & e_{1} e_{2} e_{4} & 0 & 0 & N e_{1} e_{2} e_{4} & 0 & N e_{1} e_{2} e_{4} & N e_{1} e_{2} e_{4} & N^{2} e_{1} e_{2} e_{4} & 0 & 0 & 0 & 0 & 0 & 0 & 0 & e_{1} e_{2} e_{4} & 0 & 0 & 0 & 0 & 0 & 0 & -e_{1} e_{2} e_{4} & 0 & N e_{1} e_{2} e_{4} & 0 & 0 & 0 & -N e_{1} e_{2} e_{4} & 0 & 0 & -N e_{1} e_{2} e_{4} & 0 & -N e_{1} e_{2} e_{4} & 0 & -N^{2} e_{1} e_{2} e_{4} & 0 & -N^{2} e_{1} e_{2} e_{4} & -N^{2} e_{1} e_{2} e_{4} & -N^{3} e_{1} e_{2} e_{4} \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & e_{1} e_{3} e_{4} & 0 & -N e_{1} e_{3} e_{4} & 0 & 0 & 0 & 0 & 0 & 0 & -e_{1} e_{3} e_{4} & -e_{1} e_{3} e_{4} & 0 & 0 & 0 & N e_{1} e_{3} e_{4} & N e_{1} e_{3} e_{4} & 0 & N e_{1} e_{3} e_{4} & N^{2} e_{1} e_{3} e_{4} & 0 & 0 & 0 & 0 & 0 & 0 & 0 & -e_{1} e_{3} e_{4} & -e_{1} e_{3} e_{4} & 0 & e_{1} e_{3} e_{4} & 0 & -e_{1} e_{3} e_{4} & 0 & 0 & 0 & N e_{1} e_{3} e_{4} & 0 & -N e_{1} e_{3} e_{4} & 0 & 0 & 0 & 0 & -N e_{1} e_{3} e_{4} & -N e_{1} e_{3} e_{4} & 0 & 0 & -N^{2} e_{1} e_{3} e_{4} & -N^{2} e_{1} e_{3} e_{4} & 0 & -N^{2} e_{1} e_{3} e_{4} & -N^{3} e_{1} e_{3} e_{4} \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & e_{2} e_{3} e_{4} & -N e_{2} e_{3} e_{4} & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & -e_{2} e_{3} e_{4} & -e_{2} e_{3} e_{4} & -e_{2} e_{3} e_{4} & N e_{2} e_{3} e_{4} & N e_{2} e_{3} e_{4} & N e_{2} e_{3} e_{4} & 0 & N^{2} e_{2} e_{3} e_{4} & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & -e_{2} e_{3} e_{4} & 0 & e_{2} e_{3} e_{4} & 0 & e_{2} e_{3} e_{4} & e_{2} e_{3} e_{4} & N e_{2} e_{3} e_{4} & 0 & -N e_{2} e_{3} e_{4} & 0 & -N e_{2} e_{3} e_{4} & -N e_{2} e_{3} e_{4} & 0 & 0 & 0 & 0 & 0 & -N^{2} e_{2} e_{3} e_{4} & -N^{2} e_{2} e_{3} e_{4} & -N^{2} e_{2} e_{3} e_{4} & 0 & -N^{3} e_{2} e_{3} e_{4} \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & e_{1} e_{2} e_{3} e_{4} & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & -e_{1} e_{2} e_{3} e_{4} & -e_{1} e_{2} e_{3} e_{4} & -e_{1} e_{2} e_{3} e_{4} & -e_{1} e_{2} e_{3} e_{4} & -N e_{1} e_{2} e_{3} e_{4} & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & -e_{1} e_{2} e_{3} e_{4} & 0 & e_{1} e_{2} e_{3} e_{4} & 0 & e_{1} e_{2} e_{3} e_{4} & e_{1} e_{2} e_{3} e_{4} & 0 & e_{1} e_{2} e_{3} e_{4} & e_{1} e_{2} e_{3} e_{4} & e_{1} e_{2} e_{3} e_{4} & 0 & N e_{1} e_{2} e_{3} e_{4} & N e_{1} e_{2} e_{3} e_{4} & N e_{1} e_{2} e_{3} e_{4} & N e_{1} e_{2} e_{3} e_{4} & N^{2} e_{1} e_{2} e_{3} e_{4} \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & e_{5} & -N e_{5} & 0 & 0 & 0 & N^{2} e_{5} & 0 & 0 & 0 & 0 & 0 & -N^{3} e_{5} & -N^{3} e_{5} & -N^{3} e_{5} & -N^{3} e_{5} & N^{4} e_{5} & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & -N^{4} e_{5} & 0 & 0 & 0 & 0 & -N^{5} e_{5} \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & e_{1} e_{5} & -e_{1} e_{5} & -e_{1} e_{5} & -e_{1} e_{5} & -N e_{1} e_{5} & 0 & 0 & N e_{1} e_{5} & N e_{1} e_{5} & N e_{1} e_{5} & N^{2} e_{1} e_{5} & N^{2} e_{1} e_{5} & N^{2} e_{1} e_{5} & 0 & -N^{3} e_{1} e_{5} & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & N^{2} e_{1} e_{5} & 0 & 0 & 0 & N^{3} e_{1} e_{5} & 0 & 0 & 0 & N^{3} e_{1} e_{5} & N^{4} e_{1} e_{5} \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & e_{2} e_{5} & 0 & 0 & -N e_{2} e_{5} & N e_{2} e_{5} & N e_{2} e_{5} & 0 & 0 & 0 & N^{2} e_{2} e_{5} & N^{2} e_{2} e_{5} & 0 & N^{2} e_{2} e_{5} & -N^{3} e_{2} e_{5} & 0 & 0 & 0 & 0 & 0 & -e_{2} e_{5} & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & N^{2} e_{2} e_{5} & 0 & 0 & 0 & 0 & 0 & -N^{2} e_{2} e_{5} & N^{3} e_{2} e_{5} & 0 & 0 & N^{3} e_{2} e_{5} & 0 & N^{4} e_{2} e_{5} \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & e_{3} e_{5} & 0 & 0 & -N e_{3} e_{5} & 0 & -N e_{3} e_{5} & 0 & 0 & N^{2} e_{3} e_{5} & 0 & N^{2} e_{3} e_{5} & N^{2} e_{3} e_{5} & -N^{3} e_{3} e_{5} & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & N e_{3} e_{5} & 0 & 0 & 0 & 0 & 0 & 0 & 0 & N^{2} e_{3} e_{5} & 0 & 0 & 0 & -N^{2} e_{3} e_{5} & 0 & 0 & -N^{2} e_{3} e_{5} & 0 & N^{3} e_{3} e_{5} & 0 & N^{3} e_{3} e_{5} & 0 & 0 & N^{4} e_{3} e_{5} \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & e_{4} e_{5} & 0 & 0 & -N e_{4} e_{5} & 0 & -N e_{4} e_{5} & -N e_{4} e_{5} & 0 & N^{2} e_{4} e_{5} & N^{2} e_{4} e_{5} & N^{2} e_{4} e_{5} & -N^{3} e_{4} e_{5} & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & -N^{2} e_{4} e_{5} & -N^{2} e_{4} e_{5} & -N^{2} e_{4} e_{5} & -N^{2} e_{4} e_{5} & 0 & -N^{2} e_{4} e_{5} & -N^{2} e_{4} e_{5} & 0 & 0 & N^{3} e_{4} e_{5} & N^{3} e_{4} e_{5} & 0 & 0 & 0 & N^{4} e_{4} e_{5} \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & e_{1} e_{2} e_{5} & -e_{1} e_{2} e_{5} & -e_{1} e_{2} e_{5} & -e_{1} e_{2} e_{5} & -e_{1} e_{2} e_{5} & 0 & -N e_{1} e_{2} e_{5} & -N e_{1} e_{2} e_{5} & 0 & 0 & N^{2} e_{1} e_{2} e_{5} & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & -e_{1} e_{2} e_{5} & 0 & 0 & 0 & 0 & 0 & -N e_{1} e_{2} e_{5} & 0 & 0 & -N e_{1} e_{2} e_{5} & 0 & 0 & 0 & -N^{2} e_{1} e_{2} e_{5} & 0 & 0 & -N^{2} e_{1} e_{2} e_{5} & -N^{2} e_{1} e_{2} e_{5} & -N^{3} e_{1} e_{2} e_{5} \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & e_{1} e_{3} e_{5} & 0 & 0 & 0 & -e_{1} e_{3} e_{5} & -N e_{1} e_{3} e_{5} & 0 & -N e_{1} e_{3} e_{5} & 0 & N^{2} e_{1} e_{3} e_{5} & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & -e_{1} e_{3} e_{5} & 0 & -e_{1} e_{3} e_{5} & 0 & 0 & 0 & e_{1} e_{3} e_{5} & 0 & -N e_{1} e_{3} e_{5} & 0 & 0 & 0 & N e_{1} e_{3} e_{5} & -N e_{1} e_{3} e_{5} & 0 & 0 & 0 & -N^{2} e_{1} e_{3} e_{5} & 0 & -N^{2} e_{1} e_{3} e_{5} & 0 & -N^{2} e_{1} e_{3} e_{5} & -N^{3} e_{1} e_{3} e_{5} \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & e_{1} e_{4} e_{5} & 0 & 0 & 0 & 0 & -N e_{1} e_{4} e_{5} & -N e_{1} e_{4} e_{5} & 0 & N^{2} e_{1} e_{4} e_{5} & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & e_{1} e_{4} e_{5} & e_{1} e_{4} e_{5} & e_{1} e_{4} e_{5} & e_{1} e_{4} e_{5} & 0 & 0 & N e_{1} e_{4} e_{5} & N e_{1} e_{4} e_{5} & N e_{1} e_{4} e_{5} & N e_{1} e_{4} e_{5} & 0 & 0 & 0 & 0 & 0 & -N^{2} e_{1} e_{4} e_{5} & -N^{2} e_{1} e_{4} e_{5} & 0 & 0 & -N^{2} e_{1} e_{4} e_{5} & -N^{3} e_{1} e_{4} e_{5} \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & e_{2} e_{3} e_{5} & 0 & 0 & -N e_{2} e_{3} e_{5} & 0 & 0 & -N e_{2} e_{3} e_{5} & N^{2} e_{2} e_{3} e_{5} & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & e_{2} e_{3} e_{5} & 0 & e_{2} e_{3} e_{5} & 0 & 0 & 0 & -N e_{2} e_{3} e_{5} & 0 & -N e_{2} e_{3} e_{5} & 0 & 0 & 0 & 0 & N e_{2} e_{3} e_{5} & N e_{2} e_{3} e_{5} & -N^{2} e_{2} e_{3} e_{5} & 0 & -N^{2} e_{2} e_{3} e_{5} & -N^{2} e_{2} e_{3} e_{5} & 0 & -N^{3} e_{2} e_{3} e_{5} \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & e_{2} e_{4} e_{5} & 0 & 0 & -N e_{2} e_{4} e_{5} & 0 & -N e_{2} e_{4} e_{5} & N^{2} e_{2} e_{4} e_{5} & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & -e_{2} e_{4} e_{5} & -e_{2} e_{4} e_{5} & 0 & 0 & 0 & 0 & N e_{2} e_{4} e_{5} & N e_{2} e_{4} e_{5} & 0 & 0 & 0 & N e_{2} e_{4} e_{5} & N e_{2} e_{4} e_{5} & 0 & N e_{2} e_{4} e_{5} & -N^{2} e_{2} e_{4} e_{5} & -N^{2} e_{2} e_{4} e_{5} & 0 & -N^{2} e_{2} e_{4} e_{5} & 0 & -N^{3} e_{2} e_{4} e_{5} \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & e_{3} e_{4} e_{5} & 0 & 0 & -N e_{3} e_{4} e_{5} & -N e_{3} e_{4} e_{5} & N^{2} e_{3} e_{4} e_{5} & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & -e_{3} e_{4} e_{5} & -e_{3} e_{4} e_{5} & -e_{3} e_{4} e_{5} & 0 & 0 & 0 & N e_{3} e_{4} e_{5} & N e_{3} e_{4} e_{5} & N e_{3} e_{4} e_{5} & N e_{3} e_{4} e_{5} & N e_{3} e_{4} e_{5} & N e_{3} e_{4} e_{5} & 0 & -N^{2} e_{3} e_{4} e_{5} & -N^{2} e_{3} e_{4} e_{5} & -N^{2} e_{3} e_{4} e_{5} & 0 & 0 & -N^{3} e_{3} e_{4} e_{5} \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & e_{1} e_{2} e_{3} e_{5} & 0 & 0 & 0 & -N e_{1} e_{2} e_{3} e_{5} & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & e_{1} e_{2} e_{3} e_{5} & 0 & e_{1} e_{2} e_{3} e_{5} & 0 & 0 & e_{1} e_{2} e_{3} e_{5} & 0 & 0 & 0 & N e_{1} e_{2} e_{3} e_{5} & 0 & N e_{1} e_{2} e_{3} e_{5} & N e_{1} e_{2} e_{3} e_{5} & N e_{1} e_{2} e_{3} e_{5} & N^{2} e_{1} e_{2} e_{3} e_{5} \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & e_{1} e_{2} e_{4} e_{5} & 0 & 0 & -N e_{1} e_{2} e_{4} e_{5} & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & -e_{1} e_{2} e_{4} e_{5} & -e_{1} e_{2} e_{4} e_{5} & 0 & 0 & 0 & 0 & 0 & 0 & 0 & N e_{1} e_{2} e_{4} e_{5} & N e_{1} e_{2} e_{4} e_{5} & 0 & N e_{1} e_{2} e_{4} e_{5} & N e_{1} e_{2} e_{4} e_{5} & N^{2} e_{1} e_{2} e_{4} e_{5} \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & e_{1} e_{3} e_{4} e_{5} & 0 & -N e_{1} e_{3} e_{4} e_{5} & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & -e_{1} e_{3} e_{4} e_{5} & -e_{1} e_{3} e_{4} e_{5} & -e_{1} e_{3} e_{4} e_{5} & 0 & 0 & 0 & 0 & N e_{1} e_{3} e_{4} e_{5} & N e_{1} e_{3} e_{4} e_{5} & N e_{1} e_{3} e_{4} e_{5} & 0 & N e_{1} e_{3} e_{4} e_{5} & N^{2} e_{1} e_{3} e_{4} e_{5} \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & e_{2} e_{3} e_{4} e_{5} & -N e_{2} e_{3} e_{4} e_{5} & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & -e_{2} e_{3} e_{4} e_{5} & -e_{2} e_{3} e_{4} e_{5} & -e_{2} e_{3} e_{4} e_{5} & -e_{2} e_{3} e_{4} e_{5} & N e_{2} e_{3} e_{4} e_{5} & N e_{2} e_{3} e_{4} e_{5} & N e_{2} e_{3} e_{4} e_{5} & N e_{2} e_{3} e_{4} e_{5} & 0 & N^{2} e_{2} e_{3} e_{4} e_{5} \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & e_{1} e_{2} e_{3} e_{4} e_{5} & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & -e_{1} e_{2} e_{3} e_{4} e_{5} & -e_{1} e_{2} e_{3} e_{4} e_{5} & -e_{1} e_{2} e_{3} e_{4} e_{5} & -e_{1} e_{2} e_{3} e_{4} e_{5} & -e_{1} e_{2} e_{3} e_{4} e_{5} & -N e_{1} e_{2} e_{3} e_{4} e_{5} \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & e_{6} & -N e_{6} & 0 & 0 & 0 & 0 & N^{2} e_{6} & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & -N^{3} e_{6} & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & N^{4} e_{6} & N^{4} e_{6} & N^{4} e_{6} & N^{4} e_{6} & N^{4} e_{6} & -N^{5} e_{6} \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & e_{1} e_{6} & -e_{1} e_{6} & -e_{1} e_{6} & -e_{1} e_{6} & -e_{1} e_{6} & -N e_{1} e_{6} & 0 & 0 & 0 & N e_{1} e_{6} & 0 & 0 & 0 & 0 & 0 & N^{2} e_{1} e_{6} & 0 & 0 & 0 & 0 & 0 & -N^{2} e_{1} e_{6} & -N^{2} e_{1} e_{6} & -N^{2} e_{1} e_{6} & -N^{2} e_{1} e_{6} & -N^{3} e_{1} e_{6} & -N^{3} e_{1} e_{6} & -N^{3} e_{1} e_{6} & -N^{3} e_{1} e_{6} & 0 & N^{4} e_{1} e_{6} \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & e_{2} e_{6} & 0 & 0 & 0 & -N e_{2} e_{6} & N e_{2} e_{6} & N e_{2} e_{6} & N e_{2} e_{6} & -N e_{2} e_{6} & 0 & 0 & 0 & 0 & 0 & N^{2} e_{2} e_{6} & 0 & 0 & -N^{2} e_{2} e_{6} & -N^{2} e_{2} e_{6} & -N^{2} e_{2} e_{6} & 0 & 0 & 0 & 0 & -N^{3} e_{2} e_{6} & -N^{3} e_{2} e_{6} & -N^{3} e_{2} e_{6} & 0 & -N^{3} e_{2} e_{6} & N^{4} e_{2} e_{6} \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & e_{3} e_{6} & 0 & 0 & 0 & -N e_{3} e_{6} & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & N^{2} e_{3} e_{6} & -N^{2} e_{3} e_{6} & -N^{2} e_{3} e_{6} & 0 & 0 & 0 & 0 & 0 & 0 & 0 & -N^{3} e_{3} e_{6} & -N^{3} e_{3} e_{6} & 0 & -N^{3} e_{3} e_{6} & -N^{3} e_{3} e_{6} & N^{4} e_{3} e_{6} \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & e_{4} e_{6} & 0 & 0 & 0 & -N e_{4} e_{6} & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & N^{2} e_{4} e_{6} & 0 & N^{2} e_{4} e_{6} & 0 & 0 & N^{2} e_{4} e_{6} & 0 & 0 & 0 & -N^{3} e_{4} e_{6} & 0 & -N^{3} e_{4} e_{6} & -N^{3} e_{4} e_{6} & -N^{3} e_{4} e_{6} & N^{4} e_{4} e_{6} \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & e_{5} e_{6} & 0 & 0 & 0 & -N e_{5} e_{6} & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & N^{2} e_{5} e_{6} & 0 & N^{2} e_{5} e_{6} & N^{2} e_{5} e_{6} & 0 & N^{2} e_{5} e_{6} & N^{2} e_{5} e_{6} & N^{2} e_{5} e_{6} & 0 & -N^{3} e_{5} e_{6} & -N^{3} e_{5} e_{6} & -N^{3} e_{5} e_{6} & -N^{3} e_{5} e_{6} & N^{4} e_{5} e_{6} \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & e_{1} e_{2} e_{6} & -e_{1} e_{2} e_{6} & -e_{1} e_{2} e_{6} & -e_{1} e_{2} e_{6} & 0 & 0 & 0 & e_{1} e_{2} e_{6} & e_{1} e_{2} e_{6} & e_{1} e_{2} e_{6} & -N e_{1} e_{2} e_{6} & 0 & 0 & N e_{1} e_{2} e_{6} & N e_{1} e_{2} e_{6} & N e_{1} e_{2} e_{6} & N e_{1} e_{2} e_{6} & N e_{1} e_{2} e_{6} & N e_{1} e_{2} e_{6} & 0 & N^{2} e_{1} e_{2} e_{6} & N^{2} e_{1} e_{2} e_{6} & N^{2} e_{1} e_{2} e_{6} & 0 & 0 & -N^{3} e_{1} e_{2} e_{6} \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & e_{1} e_{3} e_{6} & 0 & 0 & -e_{1} e_{3} e_{6} & e_{1} e_{3} e_{6} & e_{1} e_{3} e_{6} & 0 & 0 & 0 & -N e_{1} e_{3} e_{6} & N e_{1} e_{3} e_{6} & N e_{1} e_{3} e_{6} & 0 & 0 & 0 & N e_{1} e_{3} e_{6} & N e_{1} e_{3} e_{6} & 0 & N e_{1} e_{3} e_{6} & N^{2} e_{1} e_{3} e_{6} & N^{2} e_{1} e_{3} e_{6} & 0 & N^{2} e_{1} e_{3} e_{6} & 0 & -N^{3} e_{1} e_{3} e_{6} \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & e_{1} e_{4} e_{6} & 0 & 0 & -e_{1} e_{4} e_{6} & 0 & -e_{1} e_{4} e_{6} & 0 & 0 & 0 & -N e_{1} e_{4} e_{6} & 0 & -N e_{1} e_{4} e_{6} & 0 & 0 & 0 & 0 & N e_{1} e_{4} e_{6} & N e_{1} e_{4} e_{6} & N^{2} e_{1} e_{4} e_{6} & 0 & N^{2} e_{1} e_{4} e_{6} & N^{2} e_{1} e_{4} e_{6} & 0 & -N^{3} e_{1} e_{4} e_{6} \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & e_{1} e_{5} e_{6} & 0 & 0 & -e_{1} e_{5} e_{6} & 0 & -e_{1} e_{5} e_{6} & -e_{1} e_{5} e_{6} & 0 & 0 & -N e_{1} e_{5} e_{6} & 0 & -N e_{1} e_{5} e_{6} & -N e_{1} e_{5} e_{6} & 0 & 0 & 0 & 0 & 0 & N^{2} e_{1} e_{5} e_{6} & N^{2} e_{1} e_{5} e_{6} & N^{2} e_{1} e_{5} e_{6} & 0 & -N^{3} e_{1} e_{5} e_{6} \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & e_{2} e_{3} e_{6} & -e_{2} e_{3} e_{6} & -e_{2} e_{3} e_{6} & -e_{2} e_{3} e_{6} & -e_{2} e_{3} e_{6} & 0 & -N e_{2} e_{3} e_{6} & N e_{2} e_{3} e_{6} & N e_{2} e_{3} e_{6} & N e_{2} e_{3} e_{6} & N e_{2} e_{3} e_{6} & 0 & 0 & 0 & 0 & 0 & N^{2} e_{2} e_{3} e_{6} & N^{2} e_{2} e_{3} e_{6} & 0 & 0 & N^{2} e_{2} e_{3} e_{6} & -N^{3} e_{2} e_{3} e_{6} \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & e_{2} e_{4} e_{6} & 0 & 0 & 0 & -e_{2} e_{4} e_{6} & 0 & -N e_{2} e_{4} e_{6} & 0 & 0 & 0 & N e_{2} e_{4} e_{6} & -N e_{2} e_{4} e_{6} & 0 & 0 & 0 & N^{2} e_{2} e_{4} e_{6} & 0 & N^{2} e_{2} e_{4} e_{6} & 0 & N^{2} e_{2} e_{4} e_{6} & -N^{3} e_{2} e_{4} e_{6} \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & e_{2} e_{5} e_{6} & 0 & 0 & 0 & 0 & 0 & -N e_{2} e_{5} e_{6} & 0 & 0 & 0 & 0 & -N e_{2} e_{5} e_{6} & -N e_{2} e_{5} e_{6} & 0 & 0 & N^{2} e_{2} e_{5} e_{6} & N^{2} e_{2} e_{5} e_{6} & 0 & N^{2} e_{2} e_{5} e_{6} & -N^{3} e_{2} e_{5} e_{6} \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & e_{3} e_{4} e_{6} & 0 & 0 & 0 & 0 & 0 & -N e_{3} e_{4} e_{6} & 0 & 0 & -N e_{3} e_{4} e_{6} & 0 & 0 & 0 & N^{2} e_{3} e_{4} e_{6} & 0 & 0 & N^{2} e_{3} e_{4} e_{6} & N^{2} e_{3} e_{4} e_{6} & -N^{3} e_{3} e_{4} e_{6} \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & e_{3} e_{5} e_{6} & 0 & 0 & 0 & 0 & 0 & -N e_{3} e_{5} e_{6} & 0 & 0 & -N e_{3} e_{5} e_{6} & 0 & -N e_{3} e_{5} e_{6} & 0 & N^{2} e_{3} e_{5} e_{6} & 0 & N^{2} e_{3} e_{5} e_{6} & N^{2} e_{3} e_{5} e_{6} & -N^{3} e_{3} e_{5} e_{6} \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & e_{4} e_{5} e_{6} & 0 & 0 & 0 & 0 & 0 & -N e_{4} e_{5} e_{6} & 0 & 0 & -N e_{4} e_{5} e_{6} & -N e_{4} e_{5} e_{6} & 0 & 0 & N^{2} e_{4} e_{5} e_{6} & N^{2} e_{4} e_{5} e_{6} & N^{2} e_{4} e_{5} e_{6} & -N^{3} e_{4} e_{5} e_{6} \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & e_{1} e_{2} e_{3} e_{6} & -e_{1} e_{2} e_{3} e_{6} & -e_{1} e_{2} e_{3} e_{6} & -e_{1} e_{2} e_{3} e_{6} & -e_{1} e_{2} e_{3} e_{6} & 0 & -e_{1} e_{2} e_{3} e_{6} & -e_{1} e_{2} e_{3} e_{6} & 0 & 0 & -N e_{1} e_{2} e_{3} e_{6} & -N e_{1} e_{2} e_{3} e_{6} & 0 & 0 & 0 & N^{2} e_{1} e_{2} e_{3} e_{6} \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & e_{1} e_{2} e_{4} e_{6} & 0 & 0 & 0 & -e_{1} e_{2} e_{4} e_{6} & 0 & 0 & -e_{1} e_{2} e_{4} e_{6} & 0 & -N e_{1} e_{2} e_{4} e_{6} & 0 & -N e_{1} e_{2} e_{4} e_{6} & 0 & 0 & N^{2} e_{1} e_{2} e_{4} e_{6} \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & e_{1} e_{2} e_{5} e_{6} & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & -N e_{1} e_{2} e_{5} e_{6} & -N e_{1} e_{2} e_{5} e_{6} & 0 & 0 & N^{2} e_{1} e_{2} e_{5} e_{6} \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & e_{1} e_{3} e_{4} e_{6} & 0 & 0 & 0 & 0 & 0 & -e_{1} e_{3} e_{4} e_{6} & -N e_{1} e_{3} e_{4} e_{6} & 0 & 0 & -N e_{1} e_{3} e_{4} e_{6} & 0 & N^{2} e_{1} e_{3} e_{4} e_{6} \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & e_{1} e_{3} e_{5} e_{6} & 0 & 0 & 0 & 0 & 0 & 0 & -N e_{1} e_{3} e_{5} e_{6} & 0 & -N e_{1} e_{3} e_{5} e_{6} & 0 & N^{2} e_{1} e_{3} e_{5} e_{6} \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & e_{1} e_{4} e_{5} e_{6} & 0 & 0 & 0 & 0 & 0 & 0 & -N e_{1} e_{4} e_{5} e_{6} & -N e_{1} e_{4} e_{5} e_{6} & 0 & N^{2} e_{1} e_{4} e_{5} e_{6} \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & e_{2} e_{3} e_{4} e_{6} & 0 & 0 & 0 & -N e_{2} e_{3} e_{4} e_{6} & 0 & 0 & 0 & -N e_{2} e_{3} e_{4} e_{6} & N^{2} e_{2} e_{3} e_{4} e_{6} \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & e_{2} e_{3} e_{5} e_{6} & 0 & 0 & 0 & -N e_{2} e_{3} e_{5} e_{6} & 0 & 0 & -N e_{2} e_{3} e_{5} e_{6} & N^{2} e_{2} e_{3} e_{5} e_{6} \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & e_{2} e_{4} e_{5} e_{6} & 0 & 0 & 0 & -N e_{2} e_{4} e_{5} e_{6} & 0 & -N e_{2} e_{4} e_{5} e_{6} & N^{2} e_{2} e_{4} e_{5} e_{6} \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & e_{3} e_{4} e_{5} e_{6} & 0 & 0 & 0 & -N e_{3} e_{4} e_{5} e_{6} & -N e_{3} e_{4} e_{5} e_{6} & N^{2} e_{3} e_{4} e_{5} e_{6} \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & e_{1} e_{2} e_{3} e_{4} e_{6} & 0 & 0 & 0 & 0 & -N e_{1} e_{2} e_{3} e_{4} e_{6} \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & e_{1} e_{2} e_{3} e_{5} e_{6} & 0 & 0 & 0 & -N e_{1} e_{2} e_{3} e_{5} e_{6} \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & e_{1} e_{2} e_{4} e_{5} e_{6} & 0 & 0 & -N e_{1} e_{2} e_{4} e_{5} e_{6} \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & e_{1} e_{3} e_{4} e_{5} e_{6} & 0 & -N e_{1} e_{3} e_{4} e_{5} e_{6} \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & e_{2} e_{3} e_{4} e_{5} e_{6} & -N e_{2} e_{3} e_{4} e_{5} e_{6} \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & e_{1} e_{2} e_{3} e_{4} e_{5} e_{6} \end{array}\right)$$

開放探討¶

• 對於現在擴展維納的問題都是$n=2$或者是$n=3$時候的模板題，對於更高維的情況，可以編寫自動化的腳本來完整自動選擇關係、自動構造格等步驟，比如上述內容就是自動生成的。但是對於$n$每增加1，矩陣則是指數倍增加，因爲這是一個$2^n * 2^n$的矩陣，這時候直接調用sagemath中的LLL()變得非常緩慢，大約$n=8$的情況已經運行不出來了，我曾嘗試尋找LLL在CUDA上的並行算法或是一些其他優化方案實現，但是都是找到了論文沒有給出源碼的情況。

  如果您對這方面有所研究或者有什麼更好的優化方法，歡迎聯繫我（Xenny）一起進行更加深入的探討。

EXP¶

• 考慮到不是每個人都需要深入研究擴展維納攻擊，這裏還是給出$n=2$時候的EXP以供使用

  e1 = ...
  e2 = ...
  N = ...
  a = 5/14
  D = diagonal_matrix(ZZ, [N, int(N^(1/2)), int(N^(1+a)), 1])
  M = matrix(ZZ, [[1, -N, 0, N^2], [0, e1, -e1, -e1*N], [0, 0, e2, -e2*N], [0, 0, 0, e1*e2]])*D
  L = M.LLL()
  t = vector(ZZ, L[0])
  x = t * M^(-1)
  phi = int(x[1]/x[0]*e1)
  

References¶

• Extending Wiener's Attack in the Presence of Many Decrypting Exponents
• 並行LLL算法研究綜述
• Factoring Polynomials with Rational Coefficients
• A PARALLEL JACOBI-TYPE LATTICE BASIS REDUCTION ALGORITHM